When I was a younger graduate student, I learned the greatest word in statistics —Homoscedasticity. So let’s dive in to talk about homoscedasticity, heteroscedasticity, and why it matters even when evaluating programs!

A Bit of Background

Imagine you are an archer, and you are practicing hitting the bullseye. Sometimes, your arrows hit near the center, and sometimes they fall further away. That’s kind of how data works in statistics; some data points are close to the average, while others are a bit further away.

The differences between where the arrows land and the bullseye are similar to what statisticians call “residuals” or “errors.” They are essentially the differences between the predicted value (where we aimed the arrow) and the actual value (where the arrow landed).

What is Homoscedasticity?

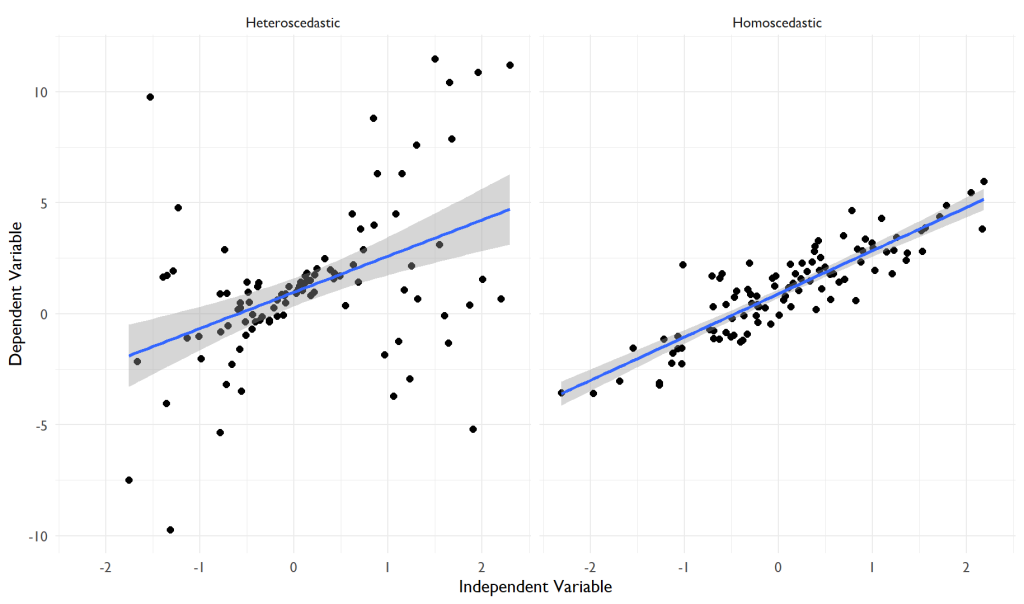
Now, let’s focus on homoscedasticity. It sounds big, but let’s break it down. ‘Homo’ means ‘same,’ and ‘scedasticity’ is about spread or scattering. So, homoscedasticity refers to a situation where the spread or scatter of the residuals (the differences between our predicted and actual values) is the same across all levels of our independent variable (the one we control or change).

For our archer example, homoscedasticity means that no matter how far or near you’re shooting from, your arrows’ spread around the bullseye remains the same.

What is Heteroscedasticity?

Heteroscedasticity, on the other hand, is when the spread of residuals is not the same across all levels of the independent variable. ‘Hetero’ means ‘different,’ so heteroscedasticity means different scatterings or spreads.

In the archery example, heteroscedasticity would mean that the spread of your arrows changes based on how far or close you’re shooting from. If you’re close, maybe your arrows are pretty close to each other around the bullseye. But if you’re far, they might spread out more, covering a wider area around the bullseye.

Why Does It Matter in Program Evaluation?

Now you might be thinking, why do we care about homoscedasticity or heteroscedasticity when evaluating programs? Well, these concepts are especially important when we’re using regression analysis to make sense of our data.

Regression analysis is like finding the best path through a mountain range (your data). If the residuals (the differences between the actual path and your best guess) are homoscedastic, it means the mountains are evenly spread out, making it easier to find a reliable path through them.

But if the residuals are heteroscedastic, it means that some parts of the mountain range are more spread out than others. This can make our path (or predictions) less reliable and lead to incorrect conclusions about our program.

When evaluating a program, knowing whether your data is homoscedastic or heteroscedastic is important. If it’s the latter, you may need to apply statistical fixes or use different techniques to ensure your conclusions about the program are as accurate and reliable as possible.

So, there you have it!